บทที่ 7
กราฟ (Graph)
กราฟ (Graph) เป็นโครงสร้างข้อมูลไม่เป็นเชิงเส้น (Nonlinear Data Structure) มีความแตกต่างจากโครงสร้างข้อมูลทรีในบทที่ผ่านมา แต่เป็นลักษณะพิเศษแบบหนี่งของกราฟโดยทรีเป็นกราฟอะไซคลิกที่ไม่มีการวนลูปและการวนถอยกลับ เป็นกราฟเชื่อมกันที่มีเพียงเอจเดียวระหว่างสองโหนด
กราฟเป็นโครงสร้างข้อมูลประเภทหนึ่งที่แสดงความสัมพันธ์ระหว่าง vertex และ edge กราฟจะประกอบด้วยกลุ่มของ vertex ซึ่งแสดงในกราฟด้วยสัญลักษณ์รูปวงกลม และ กลุ่มของ edge (เส้นเชื่อมระหว่าง vertex) ใช้แสดงถึงความสัมพันธ์ระหว่าง vertex หากมี vertex ตั้งแต่ 2 vertex ขึ้นไปมีความสัมพันธ์กัน ใช้สัญลักษณ์เส้นตรงซึ่งอาจมีหัวลูกศร หรือไม่มีก็ได้
กราฟสามารถเขียนแทนด้วยสัญลักษณ์ ดังนี้
G = ( V , E )
G คือ กราฟ
V คือ กลุ่มของ vertex
E คือ กลุ่มของ edge
ศัพท์ที่เกี่ยวข้อง
1.เวอร์เทก (Vertex) หมายถึง โหนด
2.เอดจ (Edge) หมายถึง เส้นเชื่อมของโหนด
3.ดีกรี (Degree) หมายถึง จำนวนเส้นเข้าและออก ของโหนดแต่ละโหนด
4.แอดจาเซนท์โหนด (Adjacent Node) หมายถึง โหนดที่มีการเชื่อมโยงกัน
ตัวอย่างของกราฟในชีวิตประจำวัน เช่น กราฟของการเดินทางระหว่างเมือง ซึ่ง vertex คือ กลุ่มของเมืองต่างๆ และ edge คือ เส้นทางเดินระหว่างเมือง หรือ ในเครือข่ายคอมพิวเตอร์ (Computer Network) vertex ก็คือ กลุ่มของเครื่องคอมพิวเตอร์ หรือโหนดต่างๆ และ edge ก็คือ เส้นทางการติดต่อสื่อสารระหว่างโหนดต่างๆ เป็นต้น
ประเภทของกราฟ
แบ่งเป็น 3 ประเภทโดยแบ่งตามประเภทของ edge ได้ดังนี้
1. Direct Graph (กราฟแสดงทิศทาง) เป็นกราฟที่แสดงเส้นเชื่อมระหว่าง vertex โดแสดงทิศทางของการเชื่อมต่อด้วย

2. Undirected Graph กราฟที่แสดงเส้นเชื่อมต่อระหว่าง vertex แต่ไม่แสดงทิศทางของการเชื่อมต่อ

3. Cyclic Graph กราฟที่มีเส้นเชื่อมต่อระหว่าง vertex ที่ทำให้ vertex มีลักษณะเป็นวงจรปิด (Cycle) เส้นเชื่อมต่อระหว่าง vertex อาจจะแสดงทิศทางหรือไม่แสดงทิศทางการเชื่อมต่อก็ได้

เส้นทาง (Path)
เส้นทางคือการเดินทางจาก vertex หนึ่งไปยังอีก vertex หนึ่งที่ต้องการ โดยผ่าน edge ที่เชื่อมระหว่าง vertex
ความยาวของเส้นทาง (The length of path) คือ จำนวนของ edge ในเส้นทางเดินนั้น ว่ามีจำนวนเท่าไหร่ ในการเดินทางจาก vertex หนึ่ง ไปยังอีก vertex หนึ่ง ถ้าหากเส้นทางประกอบด้วย vertex จำนวน N ความยาวของเส้นทางจะเท่ากับ N-1

ตัวอย่างเส้นทางการเดินทาง จาก vertex A ไป vertex D จะมีเส้นทางดังนี้

ตัวอย่างเส้นทางการเดินทาง จาก vertex A ไป vertex D จะมีเส้นทางดังนี้

การแทนที่กราฟด้วยเมตริกซ์
โครงสร้างข้อมูลประเภทกราฟสามารถใช้เมตริกซ์มาแสดงแทนได้ โดยกราฟที่ประกอบด้วย vertex จำนวน N vertex สามารถแทนที่ด้วยเมตริกซ์ขนาด N x N โดยค่าในเมตริกซ์จะประกอบด้วย ค่า 0 และ 1
ค่า 0 จะใช้แทนไม่มี edge ความยาว 1 เชื่อมต่อจากต้นทางไปปลายทาง และ
ค่า 1 จะใช้แทนมี edge ความยาว 1 เชื่อมต่อจากต้นทางไปปลายทาง
ตัวอย่างจากรูปกราฟแบบ Direct Graph

สามารถแทนที่กราฟด้วยเมตริกซ์ดังนี้

ตัวอย่าง หากเป็นกราฟแบบ Undirected Graph

การคำนวณเส้นทางระหว่าง vertex โดยใช้ Adjacency Matrix
จากการแทนที่กราฟด้วยเมตริกซ์ เราสามารถนำเมตริกซ์ที่ได้มาคำนวณหาจำนวนเส้นทางระหว่าง vertex ต้นทางและปลายทางที่มีจำนวน edge ต่างๆ ได้

ตัวอย่างจากรูป สามารถคำนวณจำนวนเส้นทางระหว่าง vertex ที่มี edge จำนวน 3 เส้นได้ดังนี้

ตัวอย่างจากรูป สามารถคำนวณจำนวนเส้นทางระหว่าง vertex ที่มี edge จำนวน 4 เส้นได้ดังนี้

การท่องไปในกราฟ (Graph Traversal)
การท่องไปในกราฟ (Graph traversal) คือ กระบวนการเข้าไปเยือนโหนดในกราฟ โดยใช้หลักการเดียว กับ
การเดินทางเข้าไปในทรี (Tree Traversal) คือ แต่ละโหนดจะถูกเยือนเพียงครั้งเดียว สำหรับการท่องไปในทรี
เพื่อเยือนแต่ละโหนดนั้นจะมีเส้นทางเดียว แต่ในกราฟระหว่างโหนดอาจจะมีหลายเส้นทาง เนื่องจากรูปแบบ
การเชื่อมต่อระหว่างโหนดของกราฟไม่เหมือนกับทรี สำหรับเทคนิคการท่องไปในกราฟมี 2 แบบ ดังนี้
วิธี Depth First Traversal
การท่องแบบลึก (Depth First Traversal) การทำงานคล้ายกับการท่องทีละระดับของทรี โดย
กำหนดเริ่มต้นที่โหนดแรกและเยือนโหนดถัดไปตามแนววิถีนั้นจนกระทั่งนำไปสู่ปลายวิถีนั้น จากนั้น ย้อน
กลับ (backtrack) ตามแนววิถีเดิมนั้น จนกระทั่งสามารถดำเนินการต่อเนื่องเข้าสู่แนววิถีอื่น ๆ เพื่อเยือนโหนด
อื่น ๆ ต่อไปจนครบทุกโหนด
1. กรรมวิธีท่องไปในกราฟจากจุดหนึ่งไปยังอีกจุดหนึ่งนั้นอาจทำได้หลายวิธี แต่วิธีที่นิยมใช้และง่ายก็คือการ
ท่องไปในกราฟโดยอาศัยการท่องไปบน adjacency matrix
1. สมมติว่า adjacency matrix คือดังรูป และเราจะเดินทางจาก C ไป E
1. เริ่มต้นที่แถวประจำโหนด(visit C) จากนั้นหาสมาชิกที่มีความสัมพันธ์ ซึ่งจะได้ C->A (visit A)
2. ที่แถว A ไล่ต่อไปได้ C->A->B (visit B)
3. ที่แถว B ไล่ข้าม A ที่เคย visit ข้าม C แสดงว่า แนว C->A->B ใช้ไม่ได้ (ตัน)
4. ย้อนกลับ C-A-> ข้ามB(ตัน) ข้าม C (visit แล้ว) ไปต่อ D C->A->D
5. ที่แถว D ไล่ข้าม A/C (visit แล้วทั้งคู่) ไป E ถึงปลายทาง
6. ได้ C->A->D->E เป็นคำตอบแรก
7. เราทำซ้ำต่อไปได้โดยข้ามเส้นที่เคยตัน/visit แล้ว
เราสามารถเขียนคำสั่งการทำงานออกมาได้ในลักษณะของการเรียกตนเอง และมีการอาศัย flag กำหนดบ่งบอกว่าจุดใดได้ visit ไปแล้ว (ไม่ว่าจะค้นพบหรือไม่พบเส้นทางก็ตาม) เพื่อจะไม่ไป visit ซ้ำอีก กรรมวิธีนี้อาศัยstack ของระบบในการช่วยจัดการทำงาน เนื่องจากจะมีการค้นหาลึกเข้าไปเรื่อยๆ แล้วค่อยย้อนมาคิดหนทางที่ยังค้างไว้ในภายหลัง เราจึงเรียกอัลกอริธึมแบบนี้ว่า depth-first search
วิธี Breadth First Traversal
การท่องแบบกว้าง (Breadth First Traversal) วิธีนี้ทำโดยเลือกโหนดที่เป็นจุดเริ่มต้น ต่อมาให้เยือนโหนดอื่นที่ใกล้กันกับโหนดเริ่มต้นทีละระดับจนกระทั่งเยือนหมดทุกโหนดในกราฟแทนที่จะอาศัยสแต็กเพื่อลุยหาเส้นทางย่อยจากเส้นหลัก เราอาจจะเริ่มที่ว่าเส้นทางออกจากโหนดต้นทางมีกี่เส้นทาง จากนั้นค่อยลุยหาต่อจากโหนดที่เชื่อมถัดไปนั้นจนกว่าจะพบจุดหมาย (หากซ้ำกับเส้นทางเดิมบางส่วนแล้วก็จะยกเลิกหรือตัดออกไป) กรรมวิธีนี้เราสามารถใช้คิวในการจัดการเก็บได้ เราจึงเรียกวิธีนี้ว่า breadth-first search
การท่องแบบกว้าง (Breadth First Traversal) วิธีนี้ทำโดยเลือกโหนดที่เป็นจุดเริ่มต้น ต่อมาให้เยือนโหนดอื่นที่ใกล้กันกับโหนดเริ่มต้นทีละระดับจนกระทั่งเยือนหมดทุกโหนดในกราฟแทนที่จะอาศัยสแต็กเพื่อลุยหาเส้นทางย่อยจากเส้นหลัก เราอาจจะเริ่มที่ว่าเส้นทางออกจากโหนดต้นทางมีกี่เส้นทาง จากนั้นค่อยลุยหาต่อจากโหนดที่เชื่อมถัดไปนั้นจนกว่าจะพบจุดหมาย (หากซ้ำกับเส้นทางเดิมบางส่วนแล้วก็จะยกเลิกหรือตัดออกไป) กรรมวิธีนี้เราสามารถใช้คิวในการจัดการเก็บได้ เราจึงเรียกวิธีนี้ว่า breadth-first search
1. เริ่มต้นที่แถวประจำโหนด(visit C) จากนั้นหาสมาชิกที่มีความสัมพันธ์ ซึ่งจะได้ C->A C->B C->D C->E ได้คำตอบแรกทันทีคือ C->E
2. ในกรณีที่ยังแก้ปัญหาไม่ได้ เราจะเก็บ เก็บ A B D ลงคิวในการทำแต่ละครั้ง ซึ่งตัวที่เคย visit แล้วเราจะไม่นำมาพิจารณาให้เสียเวลาต่อไปอีกในครั้งถัดไป กรรมวิธีนี้จะทำให้ได้เส้นทางที่ดีที่สุดเส้นเดียวออกมา
3. ทั้งนี้ หากต้องการหาเส้นทางที่เป็นไปได้ทั้งหมด เราอาจค้นหาต่อไปได้อีกโดยการใช้แฟล็ก (หรือจดจำตัวที่เคย visit แล้ว โดยจำเป็นลิสต์ของหนทาง และใช้ flag ประจำเส้นทางเพื่อกันไม่ได้มีการวนเส้นทางซ้ำก็อาจจะเป็นไปได้
Direct graph เป็นกราฟที่มีความสัมพันธ์ไปในทิศทางเดียว ดังรูป
เนื่องจากอัลกอริธึมค้นหาเส้นทางเป็นแบบมีทิศทาง เรายังสามารถใช้วิธีการเดิมในการหาเส้นทางได้เช่นเดียวกัน ให้สังเกตว่าตัว adjacency matrix ที่เปลี่ยนไป จะมีผลต่อผลลัพธ์ที่เกิดขึ้น
เรายังคงสามารถใช้ adjacency matrix แทนได้ โดยพิจารณาความสัมพันธ์แบบทางเดียวโดยให้ความสัมพันธ์จากหัวแถวบอกจุดเริ่มต้นดังเช่น
เรายังคงสามารถใช้ adjacency matrix แทนได้ โดยพิจารณาความสัมพันธ์แบบทางเดียวโดยให้ความสัมพันธ์จากหัวแถวบอกจุดเริ่มต้นดังเช่น
บทที่ 6
ทรี (Tree)
ทรี (Tree)ป็นโครงสร้างข้อมูลที่ความสัมพันธ์ ระหว่าง โหนดจะมัความสัมพันธ์ลดหลั่นกันเป็นลำดับ เช่น (Hierarchical Relationship) ได้มีการนำรูปแบบทรีไปประยุกต์ใช้ในงาน ต่าง ๆ อย่างแพร่หลาย สวนมากจะใชสำหรับแสดง ความสัมพันธ์ระหว่างข้อมูล เช่น แผนผังองค์ประกอบของหน่วยงานต่าง ๆ โครงสร้างสารบัญหนังสือ เป็นต้นแต่ละโหนดจะมีความสัมพันธ์กับ โหนดในระดับที่ต่ำลงมา หนึ่งระดับได้หลาย ๆโหนด เรียกโหนดดั้งกล่าวว่า โหนดแม่(Parent orMother Node)โหนดที่อยู่ต่ำกว่าโหนดแม่อยู่หนึ่งระดับเรียกว่า โหนดลูก (Child or Son Node)โหนดที่อยู่ในระดับสูงสุดและไม่มีโหนดแม่เรียกว่า โหดราก (Root Node) Data Structure โหนดที่มีโหนดแม่เป็นโหนดเดียวกัน รียกว่า โหนดพี่น้อง (Siblings)โหนดที่ไม่มีโหนดลูก เรียกว่า โหนดใบ (Leave Node)เส้นเชื่อมแสดงความสัมพันธ์ระหว่าง โหนดสองโหนดเรียกว่า กิ่ง (Branch)

นิยามของทรี
1. นิยามทรีด้วยนิยามของกราฟ ทรี คือ กราฟที่ต่อเนื่องโดยไม่มีวงจรปิด (loop)ในโครงสร้าง โหนดสองโหนด ใดๆในทรีต้องมีทางตัดต่อกันทางเดียวเท่านั้น และทรีที่มี N โหนด ต้องมีกิ่ง ทั้งหมด N-1 เส้น การเขียนรูปแบบทรี อาจเขียนได้ 4


 2. นิยามทรีด้วยรูปแบบรีเคอร์ซีฟทรีประกอบด้วยสมาชิกที่เรียกว่าโหนด โดยที่ ถ้าว่าง ไม่มีโหนดใด ๆ เรียกว่า นัลทรี (Null Tree)และถามโหนดหนึ่งเป็นโหดราก ส่วนที่เหลือจะแบ่งเป็น ทรีย่อย (Sub Tree)T1, T2, T3,…,Tk โดยที่ k>=0 และทรีย่อยต้องมีคุณสมบัติเป็นทรี
2. นิยามทรีด้วยรูปแบบรีเคอร์ซีฟทรีประกอบด้วยสมาชิกที่เรียกว่าโหนด โดยที่ ถ้าว่าง ไม่มีโหนดใด ๆ เรียกว่า นัลทรี (Null Tree)และถามโหนดหนึ่งเป็นโหดราก ส่วนที่เหลือจะแบ่งเป็น ทรีย่อย (Sub Tree)T1, T2, T3,…,Tk โดยที่ k>=0 และทรีย่อยต้องมีคุณสมบัติเป็นทรี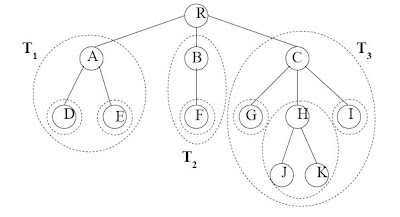 นิยามที่เกี่ยวข้องกับทรี
นิยามที่เกี่ยวข้องกับทรี
1.ฟอร์เรสต์ (Forest) หมายถึง กลุ่มของทรีที่เกิดจากการเอาโหนดรากของทรีออกหรือเซตของทรีทแยกจากกัน (Disjoint Trees)
 2.ทรีที่มีแบบแผน (Ordered Tree) หมายถึง ทรีที่โหนดต่าง ๆ ในทรีนั้นมี ความสัมพันธ์ที่แน่นอน เช่น ไปทางขวาไปทางซ้าย เป็นต้น
2.ทรีที่มีแบบแผน (Ordered Tree) หมายถึง ทรีที่โหนดต่าง ๆ ในทรีนั้นมี ความสัมพันธ์ที่แน่นอน เช่น ไปทางขวาไปทางซ้าย เป็นต้น

 2.ทรีที่มีแบบแผน (Ordered Tree) หมายถึง ทรีที่โหนดต่าง ๆ ในทรีนั้นมี ความสัมพันธ์ที่แน่นอน เช่น ไปทางขวาไปทางซ้าย เป็นต้น
2.ทรีที่มีแบบแผน (Ordered Tree) หมายถึง ทรีที่โหนดต่าง ๆ ในทรีนั้นมี ความสัมพันธ์ที่แน่นอน เช่น ไปทางขวาไปทางซ้าย เป็นต้น
3.ทรีคล้าย (Similar Tree) คือทรีที่มีโครงสร้างเหมือนกันหรือทรีที่มีรูปร่างของทรีเหมือนกันโดยไม่คำนึงถึงข้อมูลที่อยู่ในแต่ละโหนด 4.ทรีเหมือน (Equivalent Tree) คือ ทรีที่เหมือนกันโดยสมบูรณ์โดยต้องเป็นทรีที่คล้ายกันและแต่ละโหนดในตำแหน่งเดียวกันมีข้อมูลเหมือนกัน
4.ทรีเหมือน (Equivalent Tree) คือ ทรีที่เหมือนกันโดยสมบูรณ์โดยต้องเป็นทรีที่คล้ายกันและแต่ละโหนดในตำแหน่งเดียวกันมีข้อมูลเหมือนกัน
 4.ทรีเหมือน (Equivalent Tree) คือ ทรีที่เหมือนกันโดยสมบูรณ์โดยต้องเป็นทรีที่คล้ายกันและแต่ละโหนดในตำแหน่งเดียวกันมีข้อมูลเหมือนกัน
4.ทรีเหมือน (Equivalent Tree) คือ ทรีที่เหมือนกันโดยสมบูรณ์โดยต้องเป็นทรีที่คล้ายกันและแต่ละโหนดในตำแหน่งเดียวกันมีข้อมูลเหมือนกัน
5.กำลัง (Degree) หมายถึงจำนวนทรีย่อยของโหนด นั้น ๆ เช่น ในรูปโหนด “B” มีกำลังเป็น 1 เพราะมีทรีย่อย คือ {“D”}ส่วนโหนด “C” มีค่ากำลังเป็นสองเพราะมีทรีย่อย คือ {“E”, “G”, “H”, “I”} และ {“F”}
ในรูปโหนด “B” มีกำลังเป็น 1 เพราะมีทรีย่อย คือ {“D”}ส่วนโหนด “C” มีค่ากำลังเป็นสองเพราะมีทรีย่อย คือ {“E”, “G”, “H”, “I”} และ {“F”}
 ในรูปโหนด “B” มีกำลังเป็น 1 เพราะมีทรีย่อย คือ {“D”}ส่วนโหนด “C” มีค่ากำลังเป็นสองเพราะมีทรีย่อย คือ {“E”, “G”, “H”, “I”} และ {“F”}
ในรูปโหนด “B” มีกำลังเป็น 1 เพราะมีทรีย่อย คือ {“D”}ส่วนโหนด “C” มีค่ากำลังเป็นสองเพราะมีทรีย่อย คือ {“E”, “G”, “H”, “I”} และ {“F”}
6.ระดับของโหนด (Level of Node) คือ ระยะทางในแนวดิ่งของโหนดนั้น ๆ ที่อยู่ห่างจากโหนดราก เมื่อกำหนดให้ โหนดรากของทรีนั้นอยู่ระดับ 1 และกิ่งแต่ละกิ่งมีความเท่ากันหมด คือ ยาวเท่ากับ 1หน่วยซึ่งระดับของโหนดจะเท่ากับจำนวนกิ่งที่น้อยที่สุดจากโหนดรากไปยังโหนดใด ๆ บวกด้วย 1และจำนวนเส้นทางตามแนวดิ่งของโหนดใด ๆ ซึ่งห่างจากโหนดราก เรียกวา ความสูง (Height)หรือความ ลึก (Depth)


การแทนที่ทรีในหน่วยความจำหลัก
การแทนที่โครงสร้างข้อมูลแบบทรีในความจำหลักจะมีพอยเตอร์เชื่อมโยงจากโหนดแม่ไปยังโหนดลูก แต่ละโหนดต้องมีลิงค์ฟิลด์เพื่อเก็บที่อยู่ของโหนดลูกต่าง ๆ นั้นคือจำนวน ลิงคฟิลด์ของแต่ละโหนดขึ้นอยู่กับจำนวนของโหนดลูกการแทนที่ทรี ซึ่งแต่ละโหนดมีจำนวนลิงค์ฟิลด์ไม่เท่ากันทำให้ยากต่อการปฏิบัติการ วิธีการแทนที่ที่ง่ายที่สุดคือ ทำให้แต่ละโหนดมีจำนวนลิงคฟิลด์เท่ากันโดยอาจใช่วิธีการต่อไปนี้
การแทนที่โครงสร้างข้อมูลแบบทรีในความจำหลักจะมีพอยเตอร์เชื่อมโยงจากโหนดแม่ไปยังโหนดลูก แต่ละโหนดต้องมีลิงค์ฟิลด์เพื่อเก็บที่อยู่ของโหนดลูกต่าง ๆ นั้นคือจำนวน ลิงคฟิลด์ของแต่ละโหนดขึ้นอยู่กับจำนวนของโหนดลูกการแทนที่ทรี ซึ่งแต่ละโหนดมีจำนวนลิงค์ฟิลด์ไม่เท่ากันทำให้ยากต่อการปฏิบัติการ วิธีการแทนที่ที่ง่ายที่สุดคือ ทำให้แต่ละโหนดมีจำนวนลิงคฟิลด์เท่ากันโดยอาจใช่วิธีการต่อไปนี้
1.โหนดแต่ละโหนดเก็บพอยเตอร์ชี้ไปยังโหนดลูก ทุกโหนด การแทนที่ทรีด้วยวิธีนี้จะให้จำนวนฟิลด์ในแต่ละ โหนดเท่ากันโดยกำหนดใหม่ขนาดเท่ากับจำนวนโหนดลูกของโหนดที่มีลูกมากที่สุด โหนดใดไม่มีโหลดลูกก็ให้ค่า พอยเตอร์ในลิงค์ฟิลด์นั้นมีค่าเป็น Null และให้ลิงค์ฟิลด์แรกเก็บค่าพอยเตอร์ชี้ไปยังโหนด ลูกลำดับ ที่หนึ่ง ลิงค์ฟิลด์ที่สองเก็บค่าพอยเตอร์ชี้ไปยังโหนดลูก ลำดับที่สองและลิงค์ฟิลด์อื่นเก็บค่าพอยเตอร์ของโหนดลูก ลำดับถัดไปเรื่อย ๆ
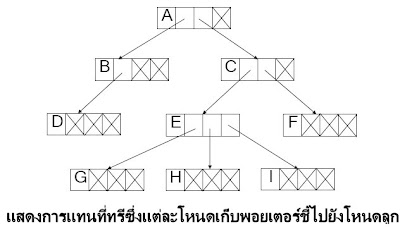

การแทนทรีด้วยโหนดขนาดเท่ากันค่อนข้างใช้เนื้อที่จำนวนมากเนื่องจากแต่ละโหนดมี จำนวนโหนดลูกไม่เท่ากันหรือบางโหนดไม่มี โหนดลูกเลยถ้าเป็นทรีที่แต่ละโหนดมีจำนวนโหนดลูกที่แตกต่างกันมากจะเป็นการสิ้นเปลือง เนื้อที่ในหน่วยความจำโดยเปล่าประโยชน์
2.แทนทรีด้วยไบนารีทรีเป็นวิธีแก้ปัญหาเพื่อลดการ สิ้นเปลืองเนื้อที่ในหน่วยความจำก็คือ กำหนดลิงค์ฟิลด์ใหม่จำนวนน้อยที่สุดเท่าที่จำเป็นเท่านั้นโดยกำหนดให้แต่ละโหนดมีจำนวนลิงค์ฟิลด์สองลิงค์ฟิลด์-ลิงค์ฟิลด์แรกเก็บที่อยู่ของโหนดลูกคนโต-ลิงค์ฟิลด์ทสองเก็บที่อยู่ของโหนดพี่น้องที่เป็นโหนดถัดไปโหนดใดไม่มีโหนดลูกหรือไม่มีโหนดพี่น้องให้ค่าพอยนเตอร์ใน ลิงค์ฟิลด์มีค่าเป็น Null



ไบนารีทรีที่ทุก ๆ โหนดมีทรีย่อยทางซ้ายและทรีย่อยทางขวา ยกเว้นโหนดใบ และโหนดใบทุกโหนดจะต้องอยู่ที่ระดับเดียวกันเรียกว่า ไบนารีทรีแบบสมบูรณ์ (complete binary tree)สามารถคำนวณจำนวนโหนดทั้งหมดในไบนารีทรีแบบสมบูรณ์ได้ถ้ากำหนดให้ Lคือระดับของโหนดใด ๆ และ N คือจำนวนโหนดทั้งหมดในทรีจะได้ว่า
ระดับ 1 มีจำนวนโหนด 1 โหนด
ระดับ 2 มีจำนวนโหนด 3 โหนด
ระดับ 3 มีจำนวนโหนด 7 โหนด
ระดับ L มีจำนวนโหนด 2L - 1โหนด
นั้นคือ จำนวนโหนดทั้งหมดในทรีสมบูรณ์ที่ มี L ระดับ สามารถคำนวณได้จากสูตรดั้งนี้

ระดับ 1 มีจำนวนโหนด 1 โหนด
ระดับ 2 มีจำนวนโหนด 3 โหนด
ระดับ 3 มีจำนวนโหนด 7 โหนด
ระดับ L มีจำนวนโหนด 2L - 1โหนด
นั้นคือ จำนวนโหนดทั้งหมดในทรีสมบูรณ์ที่ มี L ระดับ สามารถคำนวณได้จากสูตรดั้งนี้

ขั้นตอนการแปลงทรีทั่วๆ ไปให้เป็นไบนารีทรี มีลำดับขั้นตอนการแปลง ดั้งต่อไปนี้
1. ให้โหนดแม่ชี้ไปยังโหนดลูกคนโต แล้วลบความสัมพันธ์ ระหว่างโหนดแม่และโหนดลูกอื่น ๆ
2. ให้เชื่อมความสัมพันธ์ระหว่างโหนดพี่น้อง
3. จบให้ทรีย่อยทางขวาเอียงลงมา 45 องศา


การท่องไปในไบนารีทรี
ปฏิบัติการที่สำคัญในไบนารีทรี คือ การท่องไปในไบนารีทรี (Traversing Binary Tree) เพื่อเข้าไปเยือนทุก ๆโหนดในทรี ซึ่งวิธีการท่องเข้าไปต้องเป็นไปอย่างมีระบบแบบแผน สามารถเยือนโหนดทุก ๆโหนด ๆ ละหนึ่งครั้งวิธีการท่องไปนั้นมีด้วยกันหลายแบบแล้วแต่ว่าต้องการลำดับขั้นตอนการเยือนอย่างไร โหนดที่ถูกเยือนอาจเป็นโหนดแม่ (แทนด้วย N)ทรีย่อยทางซ้าย (แทนด้วย L)หรือทรีย่อยทางขวา (แทนด้วย R)
ปฏิบัติการที่สำคัญในไบนารีทรี คือ การท่องไปในไบนารีทรี (Traversing Binary Tree) เพื่อเข้าไปเยือนทุก ๆโหนดในทรี ซึ่งวิธีการท่องเข้าไปต้องเป็นไปอย่างมีระบบแบบแผน สามารถเยือนโหนดทุก ๆโหนด ๆ ละหนึ่งครั้งวิธีการท่องไปนั้นมีด้วยกันหลายแบบแล้วแต่ว่าต้องการลำดับขั้นตอนการเยือนอย่างไร โหนดที่ถูกเยือนอาจเป็นโหนดแม่ (แทนด้วย N)ทรีย่อยทางซ้าย (แทนด้วย L)หรือทรีย่อยทางขวา (แทนด้วย R)
มีวิธีการท่องเข้าไปในทรี 6 วิธี คือ NLR LNR LRN NRL RNL และ RLN แต่วิธีการท่องเข้าไปไบนารีทรีที่นิยมใช้กันมากเป็นการท่องจากซ้ายไปขวา 3 แบบแรกเท่านั้นคือ NLR LNR และ LRN ซึ่งลักษณะการนิยามเป็นนิยามแบบ รีเคอร์ซีฟ(Recursive) ซึ่งขั้นตอนการท่องไปในแต่ละแบบมีดังนี้
1. การท่องไปแบบพรีออร์เดอร์(Preorder Traversal) เป็นการเดินเข้าไปเยือนโหนดต่าง ๆ ในทรีด้วยวิธีNLR มีขั้นตอนการเดินดังต่อไปนี้
(1) เยือนโหนดราก
(2) ท่องไปในทรีย่อยทางซ้ายแบบพรีออร์เดอร์
(3) ท่องไปในทรีย่อยทางขวาแบบพรีออร์เดอร์
1. การท่องไปแบบพรีออร์เดอร์(Preorder Traversal) เป็นการเดินเข้าไปเยือนโหนดต่าง ๆ ในทรีด้วยวิธีNLR มีขั้นตอนการเดินดังต่อไปนี้
(1) เยือนโหนดราก
(2) ท่องไปในทรีย่อยทางซ้ายแบบพรีออร์เดอร์
(3) ท่องไปในทรีย่อยทางขวาแบบพรีออร์เดอร์

(1) ท่องไปในทรีย่อยทางซ้ายแบบอินออร์เดอร์
(2) เยือนโหนดราก
(3) ท่องไปในทรีย่อยทางขวาแบบอินออร์เดอร์
 3. การท่องไปแบบโพสออร์เดอร์(Postorder Traversal)เป็นการเดินเข้าไปเยือนโหนดต่าง ๆในทรีด้วยวิธี LRN มีขั้นตอนการเดินดังต่อไปนี้
3. การท่องไปแบบโพสออร์เดอร์(Postorder Traversal)เป็นการเดินเข้าไปเยือนโหนดต่าง ๆในทรีด้วยวิธี LRN มีขั้นตอนการเดินดังต่อไปนี้(1) ท่องไปในทรีย่อยทางซ้ายแบบโพสต์ออร์เดอร์
(2) ท่องไปในทรีย่อยทางขวาแบบโพสต์ออร์เดอร์

เอ็กซ์เพรสชันทรี (Expression Tree)
เป็นการนำเอาโครงสร้างทรีไปใช้เก็บนิพจน์ทางคณิตศาสตร์โดยเป็นไบนารีทรี ซึ่งแต่ละโหนดเก็บตัวดำเนินการ (Operator) และและตัวถูกดำเนินการ(Operand) ของนิพจน์คณิตศาสตร์นั้น ๆ ไว้ หรืออาจจะเก็บค่านิพจน์ทางตรรกะ (Logical Expression)นิพจน์เหล่านี้เมื่อแทนในทรีต้องคำนึงลำดับขั้นตอนในการคำนวณตามความสำคัญของเครื่องหมายด้วยโดยมีความสำคัญตามลำดับดังนี้
เป็นการนำเอาโครงสร้างทรีไปใช้เก็บนิพจน์ทางคณิตศาสตร์โดยเป็นไบนารีทรี ซึ่งแต่ละโหนดเก็บตัวดำเนินการ (Operator) และและตัวถูกดำเนินการ(Operand) ของนิพจน์คณิตศาสตร์นั้น ๆ ไว้ หรืออาจจะเก็บค่านิพจน์ทางตรรกะ (Logical Expression)นิพจน์เหล่านี้เมื่อแทนในทรีต้องคำนึงลำดับขั้นตอนในการคำนวณตามความสำคัญของเครื่องหมายด้วยโดยมีความสำคัญตามลำดับดังนี้
- ฟังก์ชัน
- วงเล็บ
- ยกกำลัง
- เครื่องหมายหน้าเลขจำนวน (unary)
- คูณ หรือ หาร
- บวก หรือ ลบ
- ถ้ามีเครื่องหมายที่ระดับเดียวกันให้ทำจากซ้ายไปขวา
การแทนนิพจน์ในเอ็กซ์เพรสชันทรี ตัวถูกดำเนินการจะเก็บอยู่ที่โหนดใบส่วนตัวดำเนินการจะเก็บในโหนดกิ่งหรือโหนดที่ไม่ใช่โหนดใบเช่น นิพจน์ A + B สามารถแทนในเอ็กซ์เพรสชันทรีได้ดังนี้
- วงเล็บ
- ยกกำลัง
- เครื่องหมายหน้าเลขจำนวน (unary)
- คูณ หรือ หาร
- บวก หรือ ลบ
- ถ้ามีเครื่องหมายที่ระดับเดียวกันให้ทำจากซ้ายไปขวา
การแทนนิพจน์ในเอ็กซ์เพรสชันทรี ตัวถูกดำเนินการจะเก็บอยู่ที่โหนดใบส่วนตัวดำเนินการจะเก็บในโหนดกิ่งหรือโหนดที่ไม่ใช่โหนดใบเช่น นิพจน์ A + B สามารถแทนในเอ็กซ์เพรสชันทรีได้ดังนี้

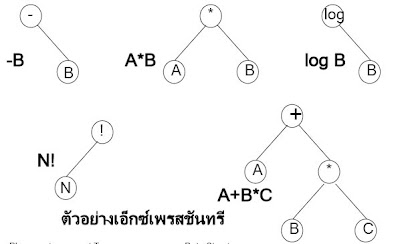
ไบนารีเซิร์ชทรี
ไบนารีเซิร์ชทรี (Binary Search Tree)เป็นไบนารีทรีที่มีคุณสมบัติที่ว่าทุก ๆ โหนดในทรี ค่าของโหนดรากมีค่ามากกว่าค่าของทุกโหนดในทรีย่อยทางซ้าย และมีค่าน้อยกว่าหรือเท่ากับค่าของทุกโหนดในทรีย่อยทางขวาและในแต่ละทรีย่อยก็มี คุณสมบัติเช่นเดียวกัน
ไบนารีเซิร์ชทรี (Binary Search Tree)เป็นไบนารีทรีที่มีคุณสมบัติที่ว่าทุก ๆ โหนดในทรี ค่าของโหนดรากมีค่ามากกว่าค่าของทุกโหนดในทรีย่อยทางซ้าย และมีค่าน้อยกว่าหรือเท่ากับค่าของทุกโหนดในทรีย่อยทางขวาและในแต่ละทรีย่อยก็มี คุณสมบัติเช่นเดียวกัน

ปฏิบัติการในไบนารีเซิร์ชทรี ปฏิบัติการเพิ่มโหนดเข้าหรือดึงโหนดออกจากไบนารีเซิร์ชทรีค่อนข้างยุ่งยากกว่าปฏิบัติการในโครงสร้างอื่น ๆเนื่องจากหลังปฏิบัติการเสร็จเรียบร้อยแล้วต้องคำนึงถึงความเป็นไบนารีเซิร์ชทรีของทรีนั้นด้วยซึ่งมีปฏิบัติการดังต่อไปนี้
(1) การเพิ่มโหนดในไบนารีเซิร์ชทรี การเพิ่มโหนดใหม่เข้าไปในไบนารีเซิร์ชทรี ถ้าทรีว่างโหนดที่เพิ่มเข้าไปก็จะเป็นโหนดรากของทรี ถ้าทรีไม่ว่างต้องทำการตรวจสอบว่าโหนดใหม่ที่เพิ่มเข้ามานั้นมีค่ามากกว่าหรือน้อยกว่าค่าที่โหนดราก ถ้ามีค่ามากกว่าหรือเท่ากันจะนำโหนดใหม่ไปเพิ่มในทรีย่อยทางขวาและถ้ามีค่าน้อยกว่านำโหนดใหม่ไปเพิ่มในทรีย่อยทางซ้ายในทรีย่อยนั้นต้องทำการเปรียบเทียบในลักษณะเดียวกันจนกระทั่งหาตำแหน่งที่สามารถเพิ่มโหนดได้ ซึ่งโหนดใหม่ที่

(2) การดึงโหนดในไบนารีเซิร์ชทรีหลังจากดึงโหนดที่ต้องการออกจากทรีแล้วทรีนั้นต้องคงสภาพไบนารีเซิร์ชทรีเหมือนเดิมก่อนที่จะทำการดึงโหนดใด ๆ ออกจากไบนารีเซิร์ชทรี ต้องค้นหาก่อนว่าโหนดที่ต้องการดึงออกอยู่ที่ตำแหน่งไหนภายในทรีและต้องทราบที่อยู่ของโหนดแม่โหนดนั้นด้วยแล้วจึงทำการดึงโหนดออกจากทรีได้ ขั้นตอนวิธีดึงโหนดออกอาจแยกพิจารณาได้ 3กรณีดังต่อไปนี้
ก. กรณีโหนดที่จะดึงออกเป็นโหนดใบการดึงโหนดใบออกในกรณีนี้ทำได้ง่ายที่สุดโดยการดึงโหนดนั้นออกได้ทันที เนื่องจากไม่กระทบกับโหนดอื่นมากนัก วิธีการก็คือให้ค่าในลิงค์ฟิลด์ของโหนดแม่ซึ่งเก็บที่อยู่ของโหนดที่ต้องการดึงออกให้มีค่าเป็น Null

 ข. กรณีโหนดที่ดึงออกมีเฉพาะทรีย่อยทางซ้ายหรือทรีย่อยทางขวาเพียงด้านใดด้านหนึ่ง วิธีการดึงโหนดนี้ออกสามารถใช้วิธีการเดียวกับการดึงโหนดออกจากลิงค์ลิสต์ โดยให้โหนดแม่ของโหนดที่จะดึงออกชี้ไปยังโหนดลูกของโหนดนั้นแทน
ข. กรณีโหนดที่ดึงออกมีเฉพาะทรีย่อยทางซ้ายหรือทรีย่อยทางขวาเพียงด้านใดด้านหนึ่ง วิธีการดึงโหนดนี้ออกสามารถใช้วิธีการเดียวกับการดึงโหนดออกจากลิงค์ลิสต์ โดยให้โหนดแม่ของโหนดที่จะดึงออกชี้ไปยังโหนดลูกของโหนดนั้นแทน
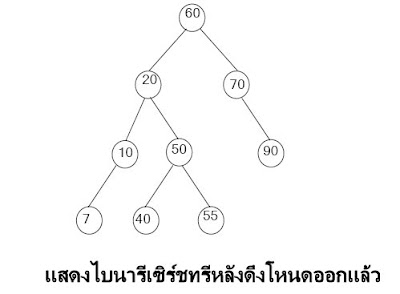
ค. กรณีโหนดที่ดึงออกมีทั้งทรีย่อยทางซ้ายและทรีย่อยทางขวาต้องเลือกโหนดมาแทนโหนดที่ถูกดึงออก โดยอาจจะเลือกมาจากทรีย่อยทางซ้ายหรือทรีย่อยทางขวาก็ได้
- ถ้าโหนดที่มาแทนที่เป็นโหนดที่เลือกจากทรีย่อยทางซ้ายต้องเลือกโหนดที่มีค่ามากที่สุดในทรีย่อยทางซ้ายนั้น
- ถ้าโหนดที่จะมาแทนที่เป็นโหนดที่เลือกมาจากทรีย่อยทางขวา ต้องเลือกโหนดที่มีค่าน้อยที่สุดในทรีย่อยทางขวานั้น
- ถ้าโหนดที่มาแทนที่เป็นโหนดที่เลือกจากทรีย่อยทางซ้ายต้องเลือกโหนดที่มีค่ามากที่สุดในทรีย่อยทางซ้ายนั้น
- ถ้าโหนดที่จะมาแทนที่เป็นโหนดที่เลือกมาจากทรีย่อยทางขวา ต้องเลือกโหนดที่มีค่าน้อยที่สุดในทรีย่อยทางขวานั้น


บทที่ 5
คิว (Queues)
คิว(Queue)เป็นโครงสร้างข้อมูลแบบเชิงเส้นหรือลิเนียร์ลิสตซึ่งการเพิ่มข้อมูลจะกระทำทีปลายข้างหนึ่งซึ่งเรียกว่าสวนท้ายหรือเรียร์ (rear)และการนำข้อมูลออกจะ กระทำที่ปลายอีกข้างหนึ่งซึ่งเรียกวา ส่วนหน้า หรือฟรอนต์(front)ลักษณะการทำงานของคิวเป็นลักษณะของการเข้าก่อน ออกก่อนหรือที่เรียกว่า FIFO (First In First Out)

การนำข้อมูลที่อยู่ตอนต้นของคิวมาแสดงจะ เรียกว่า Queue Frontแต่จะไม่ทำการเอาข้อมูลออกจากคิว การนำข้อมูลที่อยู่ตอนท้ายของคิวมาแสดงจะ เรียกว่าQueue Rear แต่จะไม่ทำการเพิ่มข้อมูลเข้าไปในคิว
การนำข้อมูลที่อยู่ตอนท้ายของคิวมาแสดงจะ เรียกว่าQueue Rear แต่จะไม่ทำการเพิ่มข้อมูลเข้าไปในคิว









การแทนที่ข้อมูลของคิวการแทนที่ข้อมูลของคิวสามารถทาได 2 วิธี คือ
1. การแทนที่ข้อมูลของคิวแบบลิงค์ลิสค์
2. การแทนที่ข้อมูลของคิวแบบอะเรย์
การแทนที่ข้อมูลของคิวแบบลิงค์ลิสต

คิว(Queue)เป็นโครงสร้างข้อมูลแบบเชิงเส้นหรือลิเนียร์ลิสตซึ่งการเพิ่มข้อมูลจะกระทำทีปลายข้างหนึ่งซึ่งเรียกว่าสวนท้ายหรือเรียร์ (rear)และการนำข้อมูลออกจะ กระทำที่ปลายอีกข้างหนึ่งซึ่งเรียกวา ส่วนหน้า หรือฟรอนต์(front)ลักษณะการทำงานของคิวเป็นลักษณะของการเข้าก่อน ออกก่อนหรือที่เรียกว่า FIFO (First In First Out)

การทำงานของคิว
การใส่สมาชิกตัวใหม่ลงในคิวเรียกว่า Enqueue ซึ่งมีรูปแบบคือenqueue (queue, newElement) หมายถึง การใส่ข้อมูลnewElement ลงไปที่ส่วนเรียร์
การนำข้อมูลที่อยู่ตอนต้นของคิวมาแสดงจะ เรียกว่า Queue Frontแต่จะไม่ทำการเอาข้อมูลออกจากคิว
 การนำข้อมูลที่อยู่ตอนท้ายของคิวมาแสดงจะ เรียกว่าQueue Rear แต่จะไม่ทำการเพิ่มข้อมูลเข้าไปในคิว
การนำข้อมูลที่อยู่ตอนท้ายของคิวมาแสดงจะ เรียกว่าQueue Rear แต่จะไม่ทำการเพิ่มข้อมูลเข้าไปในคิว








การแทนที่ข้อมูลของคิวการแทนที่ข้อมูลของคิวสามารถทาได 2 วิธี คือ
1. การแทนที่ข้อมูลของคิวแบบลิงค์ลิสค์
2. การแทนที่ข้อมูลของคิวแบบอะเรย์
การแทนที่ข้อมูลของคิวแบบลิงค์ลิสต

การแทนที่ข้อมูลของสแตกแบบลิงค์ลิสต จะประกอบไปด้วย 2 ส่วน คือ
1. Head Node จะประกอบไปด้วย 3 ส่วนคือ พอยเตอร์จำนวน 2 ตัว คือ Front และ rear กับจำนวนสมาชิกในคิว
2. Data Node จะประกอบไปด้วย ข้อมูล (Data) และพอยเตอร์ที่ชี้ไปยังข้อมูลตัวถัดไป การดำเนินการเกี่ยวกับคิวการดำเนินการเกี่ยวกับคิว ได้แก่
การดำเนินการเกี่ยวกับคิวการดำเนินการเกี่ยวกับคิว ได้แก่
1. Create Queue
2. Enqueue
3. Dequeue
4. Queue Front
5. Queue Rear
6. Empty Queue
7. Full Queue
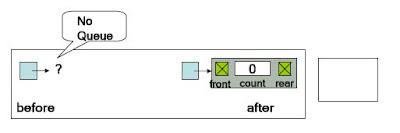 Algorithm CreateQueue
Algorithm CreateQueue
Pre Nothing
Post Head has been allocated and initialized
Return Head’s address if successful, null if overflow
1. if (memory available)
 Algorithm EnQueue
Algorithm EnQueue
Queue has been create
Post Item data have been inserted
Return Boolean; True: if successful, False ifoverflow
1. if (queue full)
1 return false
1 allocate(newPtr)
2 newPtr->data = item
3 newPtr->next = null pointer
4 if (queue->count zero)
1 queue->front = newPtr
5 else1 queue->rear->next = newPtr
6 queue->rear = newPtr
7 queue->count = queue->count+1
8 return true
End EnQueue

 Algorithm DeQueue
Algorithm DeQueue
Queue has been create
Data at front of queue returned to userthrough item and front element deleted and recycled
Return Boolean; True: if successful, False ifunderflow
1. if (queue->count is 0)
1 return false
1 item = queue->front->data
2 deleteLoc = queue->front
3 if (queue->count 1)
1 queue->rear = null pointer
4 queue->front = queue->front->next
5 queue->count = queue->count-1
6 recycle(deleteLoc)
7 return true
End Dequeue
4.Queue Front เป็นการนำข้อมูลที่อยู่ส่วนต้นของคิวมา
Algorithm QueueFront
Queue is a pointer to an initialized queue
Post Data pass back to caller
Return Boolean; True: successful, False ifunderflow
5. Queue Rear เป็นการนำข้อมูลที่อยู่ส่วนท้ายของคิวมาแสดง
Algorithm QueueRearPre
Queue is a pointer to an initialized queue
Post Data pass back to caller
Return Boolean; True: successful, False if underflow
6. Empty Queue เป็นการตรวจสอบว่าคิวว่างหรือไม่
Algorithm EmptyQueue
Queue is a pointer to a queuehead node
Return Boolean; True: if empty, False if queuehas data
1. Return (queue->count equal 0)
End EmptyQueue
7. Full Queue เป็นการตรวจสอบว่าคิวเต็มหรือไม่
Algorithm FullQueue
Pre Queue is a pointer to a queue head node
Return Boolean; True: if full, False if room for anothernode
1. allocate (tempPtr)
2. if (allocation successful)
1 release (tempPtr)
2 return false
3. else
1 return true
End FullQueue
8. Queue Count เป็นการนับจำนวนสมาชิกที่อยู่ในคิว
Algorithm QueueCount
Queue is a pointer to the queuehead node
Return Queue count
1. Return queue->count
End QueueCount
9. Destroy Queue เป็นการลบข้อมูลทั้งหมดที่อยู่ในคิว Algorithm DestroyQueue
Algorithm DestroyQueue
Queue is valid queue
All data have been deleted and recycled
Return null pointer
1. pWalker = queue->front
2. Loop(pWalker not null)
1 deletePtr = pWalker
2 pWalker = pWalker->next
3 recycle (deletePtr)
4 recycle (queue)
5 return null pointer1.
End DestroyCount
การแทนที่ข้อมูลของคิวแบบอะเรย์
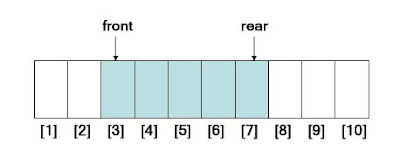 การนำข้อมูลเข้าสู่คิว จะไม่สามารถนำเข้าในขณะที่คิวเต็ม หรือไม่มีที่ว่าง ถ้าพยายาม นำเข้าจะทำให้เกิดความผิดพลาดที่เรียกว่า overflow การนำข้อมูลออกจากคิว จะไม่สามารถนำอะไรออกจากคิวที่ว่างเปล่าได้ถ้าพยายามจะทำให้เกิดความผิดพลาดที่เรียกว่า underflow ในการใส่สมาชิกลงในคิวจะต้องตรวจสอบ ก่อนว่าคิวเต็ม หรือไม่
การนำข้อมูลเข้าสู่คิว จะไม่สามารถนำเข้าในขณะที่คิวเต็ม หรือไม่มีที่ว่าง ถ้าพยายาม นำเข้าจะทำให้เกิดความผิดพลาดที่เรียกว่า overflow การนำข้อมูลออกจากคิว จะไม่สามารถนำอะไรออกจากคิวที่ว่างเปล่าได้ถ้าพยายามจะทำให้เกิดความผิดพลาดที่เรียกว่า underflow ในการใส่สมาชิกลงในคิวจะต้องตรวจสอบ ก่อนว่าคิวเต็ม หรือไม่


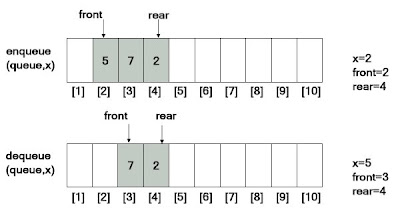 จากตัวอย่าง จะเห็นได้ว่าอาจจะมีปัญหาในการนำเข้าข้อมูลในกรณีที่คิวเต็มแต่สภาพความเป็นจริงแล้ว front ไม้ได้อยู่ในช่องแรก ของคิว จะไม่สามารถนำที่ว่างในส่วนหน้ามาใช้ได้อีก
จากตัวอย่าง จะเห็นได้ว่าอาจจะมีปัญหาในการนำเข้าข้อมูลในกรณีที่คิวเต็มแต่สภาพความเป็นจริงแล้ว front ไม้ได้อยู่ในช่องแรก ของคิว จะไม่สามารถนำที่ว่างในส่วนหน้ามาใช้ได้อีก
วิธีการแก้ปัญา ดั้งกล่าว จะใช้คิวที่เป็น แบบคิววงกลม(Circular Queue)ซึ่งคิวช่องสุดท้ายนั้นต่อกับคิวช่องแรกสุด

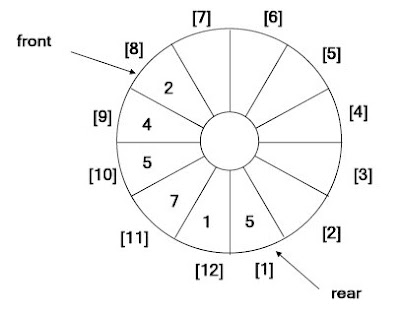
1. Head Node จะประกอบไปด้วย 3 ส่วนคือ พอยเตอร์จำนวน 2 ตัว คือ Front และ rear กับจำนวนสมาชิกในคิว
2. Data Node จะประกอบไปด้วย ข้อมูล (Data) และพอยเตอร์ที่ชี้ไปยังข้อมูลตัวถัดไป
 การดำเนินการเกี่ยวกับคิวการดำเนินการเกี่ยวกับคิว ได้แก่
การดำเนินการเกี่ยวกับคิวการดำเนินการเกี่ยวกับคิว ได้แก่1. Create Queue
2. Enqueue
3. Dequeue
4. Queue Front
5. Queue Rear
6. Empty Queue
7. Full Queue
 Algorithm CreateQueue
Algorithm CreateQueuePre Nothing
Post Head has been allocated and initialized
Return Head’s address if successful, null if overflow
1. if (memory available)
allocate (newPrt)
2 newPtr->front = null pointer
3 newPtr->rear = null pointer
4 newPtr->count = 0
5 return newPtr
2. Else1 return null pointer
End CreateQueue
2 newPtr->front = null pointer
3 newPtr->rear = null pointer
4 newPtr->count = 0
5 return newPtr
2. Else1 return null pointer
End CreateQueue

 Algorithm EnQueue
Algorithm EnQueueQueue has been create
Post Item data have been inserted
Return Boolean; True: if successful, False ifoverflow
1. if (queue full)
1 return false
1 allocate(newPtr)
2 newPtr->data = item
3 newPtr->next = null pointer
4 if (queue->count zero)
1 queue->front = newPtr
5 else1 queue->rear->next = newPtr
6 queue->rear = newPtr
7 queue->count = queue->count+1
8 return true
End EnQueue


Queue has been create
Data at front of queue returned to userthrough item and front element deleted and recycled
Return Boolean; True: if successful, False ifunderflow
1. if (queue->count is 0)
1 return false
1 item = queue->front->data
2 deleteLoc = queue->front
3 if (queue->count 1)
1 queue->rear = null pointer
4 queue->front = queue->front->next
5 queue->count = queue->count-1
6 recycle(deleteLoc)
7 return true
End Dequeue
4.Queue Front เป็นการนำข้อมูลที่อยู่ส่วนต้นของคิวมา
Algorithm QueueFront
Queue is a pointer to an initialized queue
Post Data pass back to caller
Return Boolean; True: successful, False ifunderflow
5. Queue Rear เป็นการนำข้อมูลที่อยู่ส่วนท้ายของคิวมาแสดง
Algorithm QueueRearPre
Queue is a pointer to an initialized queue
Post Data pass back to caller
Return Boolean; True: successful, False if underflow
6. Empty Queue เป็นการตรวจสอบว่าคิวว่างหรือไม่
Algorithm EmptyQueue
Queue is a pointer to a queuehead node
Return Boolean; True: if empty, False if queuehas data
1. Return (queue->count equal 0)
End EmptyQueue
7. Full Queue เป็นการตรวจสอบว่าคิวเต็มหรือไม่
Algorithm FullQueue
Pre Queue is a pointer to a queue head node
Return Boolean; True: if full, False if room for anothernode
1. allocate (tempPtr)
2. if (allocation successful)
1 release (tempPtr)
2 return false
3. else
1 return true
End FullQueue
8. Queue Count เป็นการนับจำนวนสมาชิกที่อยู่ในคิว
Algorithm QueueCount
Queue is a pointer to the queuehead node
Return Queue count
1. Return queue->count
End QueueCount
9. Destroy Queue เป็นการลบข้อมูลทั้งหมดที่อยู่ในคิว
 Algorithm DestroyQueue
Algorithm DestroyQueueQueue is valid queue
All data have been deleted and recycled
Return null pointer
1. pWalker = queue->front
2. Loop(pWalker not null)
1 deletePtr = pWalker
2 pWalker = pWalker->next
3 recycle (deletePtr)
4 recycle (queue)
5 return null pointer1.
End DestroyCount
การแทนที่ข้อมูลของคิวแบบอะเรย์
 การนำข้อมูลเข้าสู่คิว จะไม่สามารถนำเข้าในขณะที่คิวเต็ม หรือไม่มีที่ว่าง ถ้าพยายาม นำเข้าจะทำให้เกิดความผิดพลาดที่เรียกว่า overflow การนำข้อมูลออกจากคิว จะไม่สามารถนำอะไรออกจากคิวที่ว่างเปล่าได้ถ้าพยายามจะทำให้เกิดความผิดพลาดที่เรียกว่า underflow ในการใส่สมาชิกลงในคิวจะต้องตรวจสอบ ก่อนว่าคิวเต็ม หรือไม่
การนำข้อมูลเข้าสู่คิว จะไม่สามารถนำเข้าในขณะที่คิวเต็ม หรือไม่มีที่ว่าง ถ้าพยายาม นำเข้าจะทำให้เกิดความผิดพลาดที่เรียกว่า overflow การนำข้อมูลออกจากคิว จะไม่สามารถนำอะไรออกจากคิวที่ว่างเปล่าได้ถ้าพยายามจะทำให้เกิดความผิดพลาดที่เรียกว่า underflow ในการใส่สมาชิกลงในคิวจะต้องตรวจสอบ ก่อนว่าคิวเต็ม หรือไม่


 จากตัวอย่าง จะเห็นได้ว่าอาจจะมีปัญหาในการนำเข้าข้อมูลในกรณีที่คิวเต็มแต่สภาพความเป็นจริงแล้ว front ไม้ได้อยู่ในช่องแรก ของคิว จะไม่สามารถนำที่ว่างในส่วนหน้ามาใช้ได้อีก
จากตัวอย่าง จะเห็นได้ว่าอาจจะมีปัญหาในการนำเข้าข้อมูลในกรณีที่คิวเต็มแต่สภาพความเป็นจริงแล้ว front ไม้ได้อยู่ในช่องแรก ของคิว จะไม่สามารถนำที่ว่างในส่วนหน้ามาใช้ได้อีกวิธีการแก้ปัญา ดั้งกล่าว จะใช้คิวที่เป็น แบบคิววงกลม(Circular Queue)ซึ่งคิวช่องสุดท้ายนั้นต่อกับคิวช่องแรกสุด


จากตัวอย่าง จะเห็นได้ว่าอาจจะมีปัญหาในการนำเข้าข้อมูลในกรณีที่คิวเต็มแต่สภาพความเป็นจริงแล้ว front ไม้ได้อยู่ในช่องแรก ของคิว จะไม่สามารถนำที่ว่างในส่วนหน้ามาใช้ได้อีกวิธีการแก้ปัญา ดั้งกล่าว จะใช้คิวที่เป็น แบบคิววงกลม(Circular Queue)ซึ่งคิวช่องสุดท้ายนั้นต่อกับคิวช่องแรกสุด
ไม่มีความคิดเห็น:
แสดงความคิดเห็น